线性布局及通用洗牌

这几天d调研的 DSL 居然 2025 年了，还在把布局里的下标一个个列出来做分析，研究了几天布局代数，毛磊的博客可以说是其中讲得最好的。然而看完了我发现……并没有什么卵用啊，我需要的是：

• 如何计算一个布局有无重复，如何合并？
• 如何用寄存器洗牌的方法变换两个布局？
• 如何分析一个布局的内存访问模式是否最优？

这些问题并没有在 CuTe 的布局代数中得到解决。CuTe 的布局代数虽然复杂，但实际上大部分操作都只提供了布局间的组合，并没有提供布局间的求解功能。正好，Triton 团队在五月发布了线性布局的论文，这个布局我认为是真正地解决了布局代数的难题的：

• CuTe 的布局代数定义在所有的整数上，但实际上绝大多数布局相关的难题都只设计二的幂次，线性布局的这个限制影响不大。
• CuTe 的布局代数无法表达 Swizzle 布局，而线性布局可以解决。
• 线性布局顾名思义，遵循线性代数，因此可以直观地根据矩阵运算进行理解和分析，得到很多非常有意义的结论。

线性布局

那么简单介绍一下线性布局吧。由于我们已经限定了输入输出的维度都是二的幂次，因此可以直接把输入输出的各个维度分解为 2 的各个幂次的基。例如，hmma16816.f16的 A 矩阵布局：

这个布局是线程序号 t，线程中数据序号 v 到矩阵的行 i 和列 j 的映射$(T, V) \to (i, j)$。将各个量分解为 2 的幂次，则

$$\begin{bmatrix} j_1 \\ j_2 \\ j_4 \\ j_8 \\ i_1 \\ i_2 \\ i_4 \\ i_8 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \\ v_4 \\ t_1 \\ t_2 \\ t_4 \\ t_8 \\ t_{16} \end{bmatrix}$$

注意图中低位在左上，高位在右下。也就是说，通过线性布局，可以将布局代数转化为线性运算，从几乎没有理论基础的布局代数，引入到了有大量研究基础的在$\mathbb F(2)$上定义的线性代数。

并且，异或运算也是$\mathbb F(2)$上的线性运算，因此 Swizzle 也可以很好地在线性布局中表示。例如Swizzle<2, 3, 3>

这个布局在 CuTe 中需要特殊处理，而在线性布局中可以直接用

$$\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix}$$

表示，例如最后一个元素的坐标231 = 0b11100111 = 0b11111111 ^ 0b00011000。

基于线性布局分析

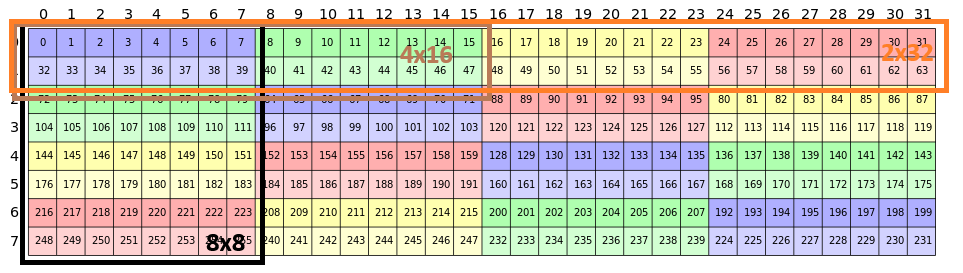
通过这样的布局，可以进行大量非常有用的计算，例如，基于上述的矩阵，进行一次 8x8 核心矩阵的访问，访问的布局为

$$\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} j_1 \\ j_2 \\ j_4 \\ 0 \\ 0 \\ i_1 \\ i_2 \\ i_4 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 &0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} j_1 \\ j_2 \\ j_4 \\ i_1 \\ i_2 \\ i_4 \end{bmatrix}$$

可以直观地看到，访问这样一个矩阵时，矩阵的左上角有一个 3x3 的单位阵，这代表这组访问每 8 个元素连续。这里一个元素的大小为两字节，那么第 2 行到第 6 行代表共享内存的 32 个 bank。这个线性布局中，这些行不为零，代表这次访问散布在各个 bank 中，没有冲突。

Swizzle 布局的意义在于按行和按若干列同时访问时没有冲突，如果需要进行 2x32 的访问，也就是在矩阵的连续维度上，则布局是一个 8x6 的单位阵，代表所有的内存访问连续，自然也是没有 bank 冲突的。

$$\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} j_1 \\ j_2 \\ j_4 \\ j_8 \\ j_{16} \\ i_1 \\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} j_1 \\ j_2 \\ j_4 \\ j_8 \\ j_{16} \\ i_1 \end{bmatrix}$$

但上述的 swizzle 要求一次要么访问 2x32 ，要么访问 8x8，如果访问 4x16 的话就不行了，有一行会变成全零，所以会产生两路冲突，这在图中也可以直接看出。

$$\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} j_1 \\ j_2 \\ j_4 \\ j_8 \\ 0 \\ i_1 \\ i_2 \\ 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 \\ \color{red}{0} & \color{red}{0} & \color{red}{0} & \color{red}{0} & \color{red}{0} & \color{red}{0} \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} j_1 \\ j_2 \\ j_4 \\ j_8 \\ i_1 \\ i_2 \end{bmatrix}$$

在 Triton 中，目前已经实现了大量的基于线性布局的算法，成为了 Triton 区别于其他 DSL 的重要特点。这也是为什么 Triton 很多操作都要求参数是 2 的幂次。

通用线程间洗牌

在 Tensor Core 编程中，一个非常繁琐的地方在于如何把寄存器按照符合硬件和算法的布局进行排布，并在各种布局间进行转换。即使是 ThunderKittens 的作者，据说也表示搞不定 fp8 布局和 fp16 布局间的转换，那么就让我们基于线性布局，研究一下这个问题。

在论文中提到了一个线程间洗牌的通用方法，并在 PR5419 中实现，然而我打开代码想学习一下，发现三周前大神 FrederickVu 在 PR7558 直接提出了更优的算法。

那么，TK 团队搞不定的布局是什么呢？实际上就是论文中图 3 的运算。图中一个框代表 4 个元素，在 fp16 运算中，一个线程占据四列，而在fp 8 中则占据 8 列，需要线程间洗牌来进行转换。

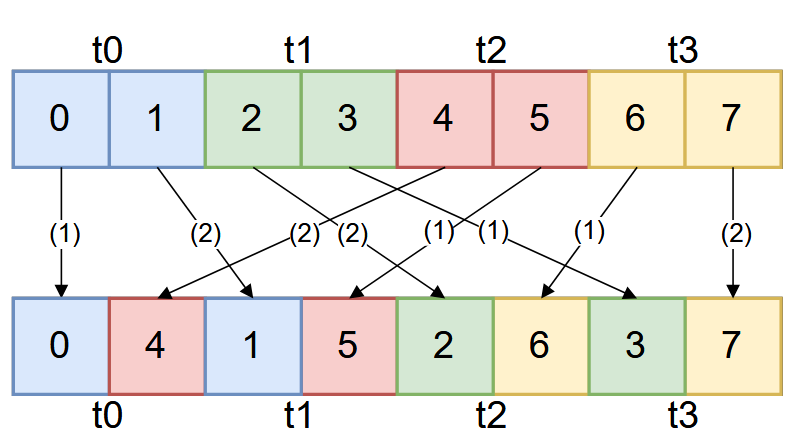
用线性布局的方法来描述，原本的布局为$A = \begin{bmatrix}1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1 \end{bmatrix}$，需要的布局为$B = \begin{bmatrix}0 & 1 & 0 \\0 & 0 & 1 \\1 & 0 & 0 \end{bmatrix}$。这里布局的定义是$\begin{bmatrix}n_1\\n_2\\n_4\end{bmatrix}=M\begin{bmatrix}r\\t_1\\t_2\end{bmatrix}$，因此我们需要找到一个转换$P=B^{-1}A=\begin{bmatrix}0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix}$来完成这个操作。

然而，这个操作并不平凡。在 CUDA 程序中，我们只能使用两种方法完成上述操作

• 寄存器内部根据线程号，条件交换若干寄存器：if (threadid & mask) swap(A, B)。
• 线程间洗牌，基于val = __shfl_sync(val, id)，在线程间交换所使用的寄存器。

这两个办法都只能对数据进行交换，并不能自主地让数据在线程间“流动”。利用手动试错可以发现，要做到上述的运算，需要后两个线程交换两次寄存器，做两次线程间洗牌，再在奇数线程交换两次寄存器。这个过程非常不显然，以至于长期都只有手动实现的算法。

然而，基于线性布局，我们可以发现：

• 寄存器内部根据线程号交换寄存器，可以实现运算$\begin{bmatrix}1 & 1 \\ 0 & 1\end{bmatrix}$，这里左上表示寄存器，右下表示线程。
• 线程间洗牌，可以实现运算$\begin{bmatrix}1 & 0 \\ 1 & 1\end{bmatrix}$，另外右下的线程部分也可以做任意的变换。

因此……非常不显然地，可以发现上述过程的最原子的操作是：两个线程间交换两个寄存器，相当于把寄存器号和线程号做了一个“反射”，即$\begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix}$。在二进制中，这个运算可以分解为

$$\begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix} = \begin{bmatrix}1 & 1 \\ 0 & 1\end{bmatrix} \begin{bmatrix}1 & 0 \\ 1 & 1\end{bmatrix} \begin{bmatrix}1 & 1 \\ 0 & 1\end{bmatrix}$$

从布局上看，依次做了条件交换r_i ^= l_j，线程间洗牌l_j ^= r_i，条件交换r_i ^= l_j，刚好，这符合了上述两种操作的矩阵布局。因此可以把$P$做分解：

$$P = \begin{bmatrix}0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix} = P_{cross} P_{lane} P_{reg} \\ = \begin{bmatrix}0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix}1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0\end{bmatrix} \begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix} \\ = \begin{bmatrix}1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix}1 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix}1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix}1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0\end{bmatrix} \begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}$$

其中$P_{reg}$是在一个线程内部对寄存器做一次和线程号无关的洗牌，一般不需要操作。而$P_{lane}$是一个抽象的“把自己的线程号换掉”的操作，只能在线程间洗牌时顺便进行。因此，需要把右边的条件交换操作和而$P_{lane}$交换位置，并把$P_{lane}$融进线程间洗牌：

$$P = \begin{bmatrix}0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix} = \begin{bmatrix}1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix} \left(\begin{bmatrix}1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0\end{bmatrix} \begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1\end{bmatrix}\right) \begin{bmatrix}1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}$$

那么，对应的代码就是：

// 0 1 | 2 3 | 4 5 | 6 7
auto tmp0 = laneid & 2 ? reg[1] : reg[0];
auto tmp1 = laneid & 2 ? reg[0] : reg[1];
// 0 1 | 2 3 | 5 4 | 7 6
int shuffle_laneid = (laneid & ~3) | ((laneid & 1) << 1) | ((laneid & 2) >> 1);
// laneid: 0 2 1 3
auto tmp2 = __shfl_sync(0xffffffff, tmp0, shuffle_laneid ^ 0);
auto tmp3 = __shfl_sync(0xffffffff, tmp1, shuffle_laneid ^ 2);
// 0 4 | 5 1 | 2 6 | 7 3
reg[0] = laneid & 1 ? tmp3 : tmp2;
reg[1] = laneid & 1 ? tmp2 : tmp3;
// 0 4 | 1 5 | 2 6 | 3 7

Triton 中相应的代码藏得很深，不好利用，我把这个过程做了一个简单的脚本，希望大家可以不再被线程间洗牌所困扰😇：melonedo/generic-intra-warp-shuffle-generator.py。

讨论

可以看到，线性布局给布局运算带来了非常大的潜力，可以实现极其复杂的分析过程，在这个过程中的 Swizzle 也能表示这一点至关重要。这样复杂的计算，显然是不适合于用 C++ 模板元编程在编译期进行计算并生成的代码的，程序员手写也非常地困难。也就是说，这属于是一种典型的编译器实现容易，而程序员实现难的问题，是编译器最舒适的区间。这样的功能，如果内置到 DSL 的编译器中，可以直接实现多对多的寄存器布局转换，会对 Tensor Core 的编程带来非常大的遍历。直白地说，或许正是因为 nvcc 没有找到合适的方法实现这些功能，才导致了 DSL 的百花齐放，在一些基本的抽象上花费大量的心思。