受到硬件特性、缓存局部性、任务特点等的约束，一个 AI 中的计算任务通常需要复杂的数据布局。所谓数据布局，包括三个方面：

  • 逻辑布局：每个元素在算法中对应的含义，例如一个元素在矩阵中的行列坐标 (m, n)，或是一个点在三维空间中的 (x, y, z) 坐标。
  • 内存布局：不管是共享内存或是全局内存，都只由一个连续的一维指针 p 索引，需要将多种多样的数据布局映射到单一的一维指针 p 上。
  • 寄存器布局：数据在计算时，需要加载到特定的线程 t 中特定的寄存器 r。寄存器布局本应该比较简单，但 Tensor Core 的硬件特性使得寄存器布局变得异常复杂。

内存布局的约束

内存布局是基本的 CUDA 编程中非常注重的一方面，受到多种约束，主要体现为全局访问合并和避免共享内存 bank 冲突两个方面。全局内存的一次访问以 32 字节为单位，而 L2 缓存的单位为 128 字节。一次请求中需要的数据会组合成多个 32 字节的请求发出，为了高效地利用全局内存的带宽，需要尽可能地按照 32 字节对齐并且连续地访问全局内存，体现到地址上要求低位地址递增。而共享内存的组织形式更为特殊，每次访问以 128 字节为单位，但要求这 128 字节中每 4 个字节对应的低位地址（bank）互不相同，否则产生 bank 冲突，需要发起多次共享内存请求。128 字节是 CUDA 内存请求的基本单位，来源是 32 个线程，每次访问一个寄存器的大小，即 4 字节。后面在 Tensor Core 中也可以看到这个 128 字节这个重要单位。

然而，上述的约束并没有得到 CUDA 编译器的直接支持，需要依赖程序员手动处理。例如，RGB 图片的格式如果是 NHWC，每个线程处理一个像素的 3 个颜色分量，则显然会写出依次读取 3 个分量的代码。这样的代码每次请求一个分量时，一个线程束（warp）需要的数据分散到 96 个字节中，需要发起 3 次全局内存请求。当然，后续访问另外两个分量时，会命中 L1 缓存，不需要访问 L2 或是显存。

Tensor Core 对寄存器布局的约束

Tensor Core 是 Volta 及以后的架构引入的矩阵计算单元。相比于之前的各种 CUDA 计算单元，Tensor Core 对一个线程束中 32 个线程的多个寄存器进行计算，各个线程的寄存器视为一个整体重新排布，打破了 SIMT 中各线程各自独立的抽象，要求程序员按照 SIMD 中的视角重新审视 CUDA 程序。

截止到 Blackwell，Tensor Core 分为 5 代，每一代都有各自的特点：

  • 第一代 Volta 第一次加入了 Tensor Core，每个 SM 有 8 个，可以计算 4x4x4 的矩阵乘法，但提供的接口是HMMA884.stepN，可以同时计算 4 组互不关联的 8x8x4 矩阵运算。这个接口太奇葩，仅存在了一代。
  • 第二代 Turing 除了加入了更多的数据类型，也修改了硬件接口为HMMA1688，对应的 PTX 接口从此一直保持兼容。
  • 第三代 Ampere 大改了架构，每个 SM 有 4 个 Tensor Core，每个计算 8x4x8 矩阵乘，吞吐翻倍。同时这时候发现寄存器的数量不够用了，因此加入了直接从全局内存读取到共享内存的LDGSTS功能。
  • 第四代 Hopper 再次性能加倍，每个 Tensor Core 的计算格式没有说明，但根据 Revealing Floating-Point Accumulation Orders in Software/Hardware Implementations，维度 K 是 16。同时这时候整个系统的吞吐都需要升级，因此引入了异步操作以及 TMA。
  • 第五代 Blackwell 性能再次翻倍，这时候 CUDA 的整个链路已经完全满足不了 Tensor Core 的需求了，Tensor Core 干脆独立，有了自己的寄存器和指令队列。

上面矩阵运算的维度表达为 MxNxK，即A[MxK] @ B[KxN] = C[MxN]。

一代太特殊，五代不让用。所以这里我们主要看第二到第四代的布局，这些布局都有共同点：

权重矩阵

权重矩阵 A 和 B 矩阵都是 K 主序，也就是 A 行主序，B 列主序。每个线程贡献一个寄存器，组成一个核心矩阵（core matrix），一个核心矩阵固定为 8 行，每行 4 个线程，一行的长度取决于这 4 个寄存器一共能放几个元素（f64例外，布局等同于f32）。例如放f16，那么 4 个线程放 8 个，核心矩阵为 8x8，如果放f8，则核心矩阵为 8x16。虽然在文档以及 CUTLASS 实现中这些矩阵的布局都是独立列出，不过实际上这些矩阵的布局都非常地固定，根据下列的分析可以直接推导出所有的布局。

mma-1688-A-f16 2 代 Tensor Core 中的mma.m16n8k8中 A 矩阵寄存器布局，每个寄存器包括两个f16，所以核心矩阵大小为 8x8，包括一上一下两个核心矩阵按照MN主序排列。

mma-16816-A-f16 3 代 Tensor Core 中的 mma.m16n8k16中 A 矩阵寄存器布局，每个寄存器包括两个f16，所以核心矩阵大小为 8x8，四个 8x8 核心矩阵按照 MN 主序排列，依次在左上、左下、右上、右下。实际上这一代 Tensor Core 的内积维度是 8，所以可以理解为这个布局仅仅是在mma.m16n8k8的基础上沿着 K 维度再执行一次。

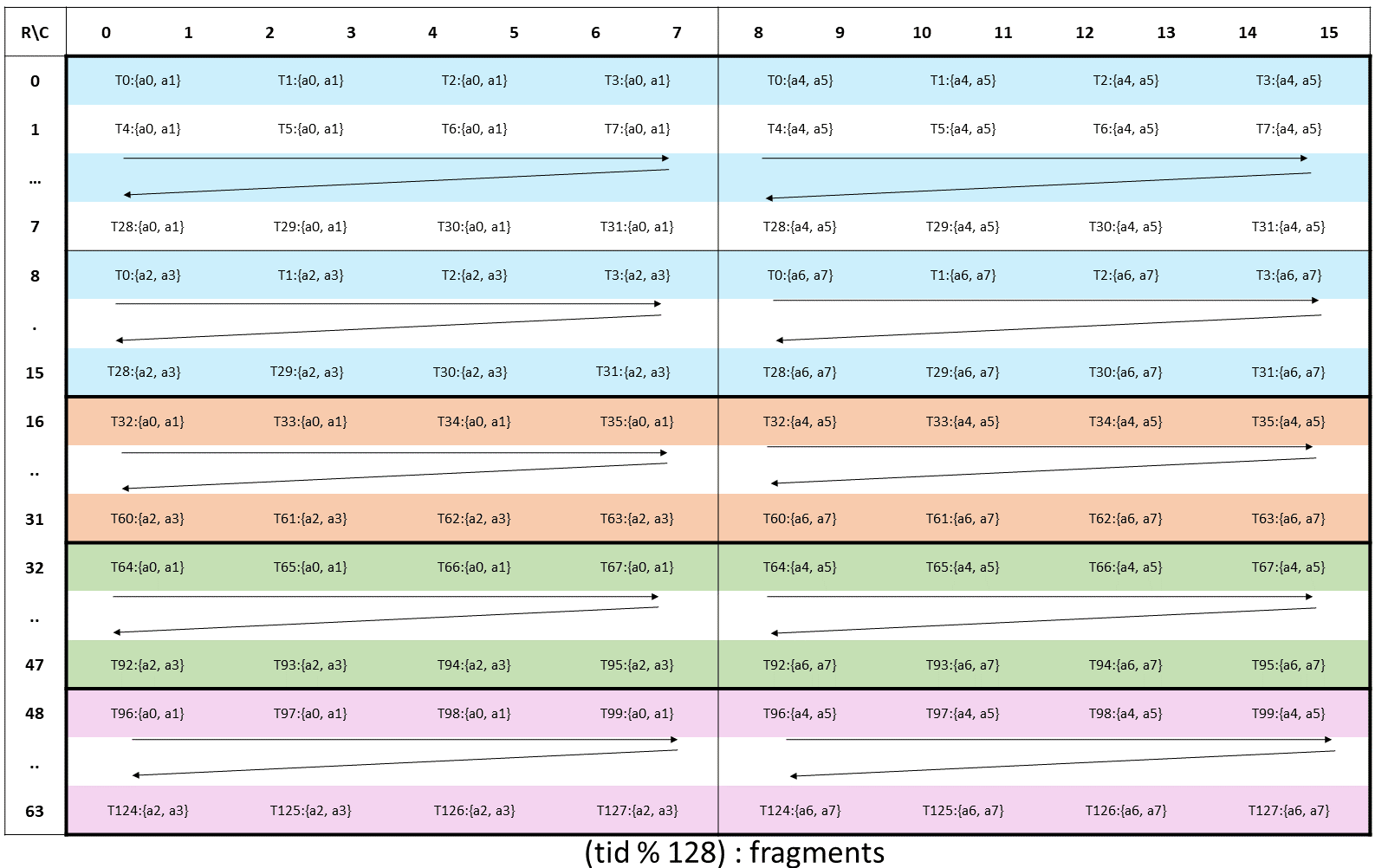wgmma-64N16-A 4 代 Tensor Core 中的 wgmma.mma_async.m64nNk16 中 A 矩阵寄存器布局中，由于是整个线程束组（warp group）都参与运算，由一个线程束贡献 4 个核心矩阵，构成和mma.m16n8k16完全一样的 16x16 布局，每个线程束再在 MN 方向排列构成 64x16 矩阵。wgmma指令从共享内存中读取数据时，大概率仍是一次读取一个核心矩阵，因此在冲突避免上的行为是完全一致的。

mma-8832-A-i4 如果是其他大小的类型，例如mma.m8n8k32中使用 4 比特的s4或者u4类型，则一行 4 线程的 4 个寄存器可以放 32 个元素，核心矩阵大小 8x32，其他方面完全相同。

图中都是 A 矩阵，由于采用了 K 布局，所以 B 矩阵的布局也是完全类似的，只不过是列主序。通过这几个矩阵的分析，可以发现 2 到 4 代 Tensor Core 的设计上非常类似，只是不断地拓展了矩阵的大小。在这个布局中，可以把线程根据低位分为 4 个 bank，A 和 B 中对应要做内积的元素都在同一 bank 中对应的位置，这显然简化了硬件中数据的布局。

累加矩阵

累加矩阵 C 和 D 矩阵布局按照行主序，每个线程依次放两个元素，每行 8 个元素，不区分数据类型，也就是f16累加时寄存器布局也相同，只不过用的寄存器数量减半。

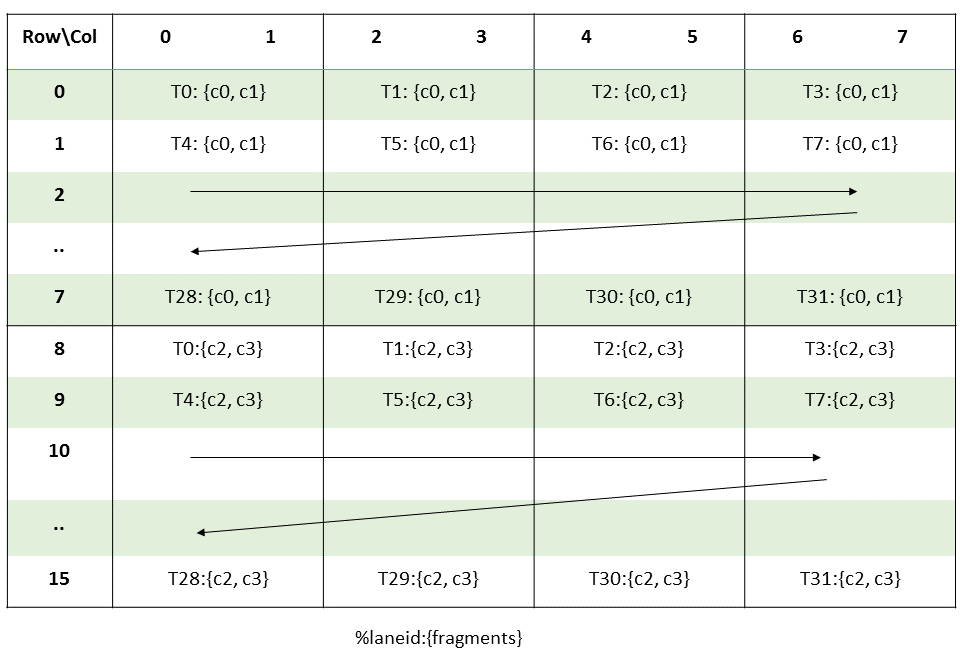mma-16816-C-f16 2 和 3 代 Tensor Core 中的 mma.m16n8kK中 C 矩阵寄存器布局，两个 8x8 矩阵构成 16x8 矩阵。mma接口中 N 维度固定为 8，一个线程束中 32 个线程刚好对应 8x8 的矩阵。

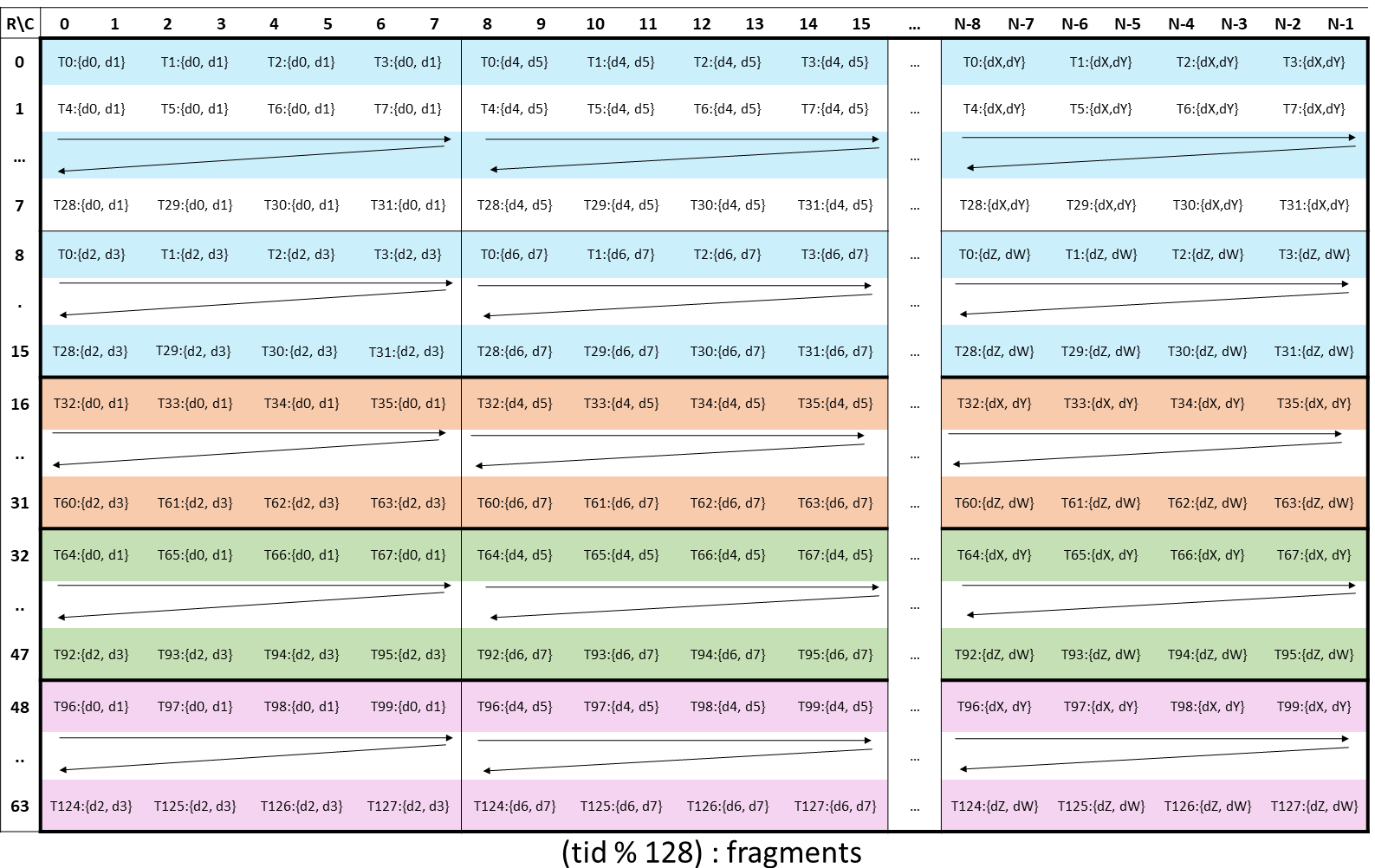wgmma-64N16-D 4 代 Tensor Core 中的 wgmma.mma_async.m64nNk16中 D 矩阵寄存器布局 和 A 矩阵布局类似，在列方向上堆叠 4 个线程束各自的 16 x 16 矩阵。wgmma接口中 M 为 64，N 为 8 的倍数，一个线程束组中 4 个线程束共 128 个线程放一个 64x8 的矩阵。

一代 Tensor Core

一代 Tensor Core 则完全不同，可以任意地选择 A 和 B 是行主序还是列主序，其中行主序指的是一个矩阵出 4 个寄存器，对应一行 4 列，4 个线程对应 4 行；列主序反之。后续的设计中把这个矩阵转置的接口转移到了ldmatrix上，支持一个线程读取的 16 字节数据分散到一行的 4 个线程。如果没有ldmatrix，则读取 16x16 的f16矩阵时各线程的访问粒度是 4 字节，必须发出 4 次 4 字节读取，而使用ldmatrix，每行的 4 个线程所需要的数据连续，只需要发出一次 16 字节读取，提高了共享内存效率。

约束求解

由于内存布局和寄存器布局两方面的约束，在进行涉及 Tensor Core 的编程时，可行并且高效的方案通常并不多，在内存方面，可以用 swizzle 比较通用地解决，而在寄存器布局方面仍然百家争鸣。

swizzle

内存布局中存在本质的冲突，即计算时不可避免地访问不连续的维度，Nsight Compute 里叫做 Strided Access。例如一个矩阵是行主序，那么连续的维度就是行，列就是不连续的维度。按照列访问矩阵，不可避免地会产生多倍的全局内存请求以及共享内存请求。当访问不连续的维度时，无法。这个问题有两种解决办法：

  • 从源头上就更改数据在全局内存的布局，改成按照访问的维度连续。然而实际上可能需要按照多个维度访问，因此通常无法使用这个方法。
  • 不改变全局内存的布局，改变共享内存中的布局。

改变共享内存的布局可以使用多补一列 padding 元素的方法，例如 MxN 矩阵，可以用 Mx(N+1) 的空间来存，这样坐标映射为(m, n) -> p = m*(N+1)+n = m*N+(m+n)，满足内存布局约束。而更优雅的方法是在占据空间不变的情况下，重新映射共享内存的布局。仍以 MxN 为例，我们可以按照 Mx(N+1) 来计算坐标，但为了避免坐标溢出到下一行，把行坐标按照实际的列数取模，计算公式为(m, n) -> p = m*N + (m+n)%N。在 N 是二的幂次时，可以把这个加法再取模的运算换成等价的异或，就得到了 swizzle 布局。关于 swizzle 的具体计算网上有大量的文章，不再赘述，例如 reed 大神的 cute 之 Swizzle。

由于 swizzle 已经基本成为 CUDA 编程中内存布局的通解，因此英伟达把这个方案固化到了硬件当中。不管是用用 TMA、wgmma或是ldmatrix加载矩阵时，都是以一次一个核心矩阵的形式加载的，没有额外的内存合并单元。在全局内存中如果矩阵简单按照行主序或是列主序排列，每次都无法完全访问连续维度，需要用 swizzle 的方法解决。 wgmma接口以及 TMA 都支持指定 swizzle 的数据格式，分别支持一行的长度为 16、32、64、128 字节的矩阵。

以f16类型，即 2 字节元素为例，每次读取一个 8x8 的核心矩阵，一行的长度为 16 字节，需要读取 8 行。图中将核心矩阵连续读取的 4 个 bank 为一组用同一种颜色表示，不同的颜色表示不同的 bank 组，可见每个 8x8 核心矩阵的 8 行颜色互不相同，这说明不同的 swizzle 模式分别用于从一行的长度为 16、32、64、128 字节的矩阵中一次读取一个核心矩阵时避免 bank 冲突。

K 主序 16 字节 swizzle：Swizzle-16B-16b-K-Major

K 主序 32 字节 swizzle：Swizzle-32B-16b-K-Major

K 主序 64 字节 swizzle：Swizzle-64B-16b-K-Major

K 主序 128 字节 swizzle：Swizzle-128B-16b-K-Major

这里只画了一行核心矩阵，继续往下画没有意义。MN 主序在读取时会再转置一下，没有本质区别，例如 2 字节元素 MN 主序 32 字节 swizzle，两列核心矩阵：Swizzle-32B-16b-MN-Major。

PTX 文档吐槽

128 字节 swizzle 实在是太长了，把一个格的大小改成 16 字节元素表示吧：Swizzle-128B-128b-K-Major

上图就是现在 PTX 文档中的图片，这个图片只能说勉强能看，没注意的还以为他是在一个核心矩阵的范围内 swizzle 呢。

PTX 文档的图片有过更新，以前是一堆非常神奇的图片，比如 GPUs Go Brrr 里面怒骂的这张图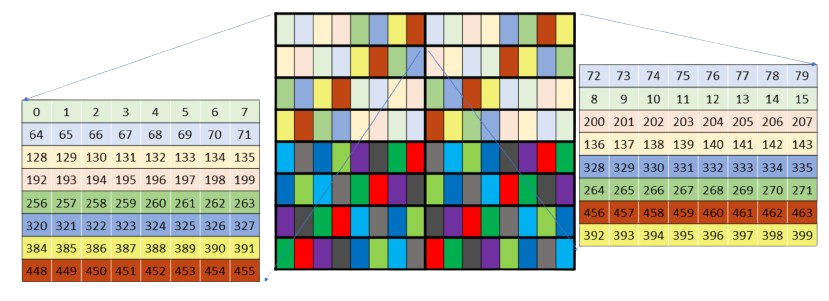：Swizzle-128B-16b-K-Major-False

仔细看看，实际上是前面的 2 字节元素 K 主序 32 字节 swizzle 图的前两组 bank，但他把每个 bank 的元素都写到一列里了，用颜色表示原本在第几个核心矩阵。 Swizzle-128B-16b-K-Major-64x8

这已经是旧版 PTX 里面比较正常的图了，还有很多更离谱的。不过好在现在 PTX 已经投降，直接把 CUTLASS 布局写出来了。只不过画的图依然是非常地离谱，比如PTX 文档的 2 字节元素 MN 主序 32 字节 swizzle 图片用的颜色简直是画蛇添足。

寄存器布局代数

Tensor Core 对寄存器的分布提出了非常严格的约束，使得很多基于逻辑分布进行的计算都极为复杂，需要依赖布局代数（layout algebra）解决。布局代数也是 CUTLASS 库的核心功能，可以根据要求，将各种布局进行变换并进行可视化，满足算法的需求。然而提供布局变换只是工具，更困难的问题是选择什么布局。例如 ThunderKittens 就对在寄存器中存放的矩阵/向量提供了多种布局可供选择，某些布局似乎还会复制多份副本来加速运算。而更激进的方法是像 Triton 一样，直接让编译器决定用什么布局，用户只根据逻辑布局编写算法，寄存器布局和内存布局无法控制。而 CUDA 在这方面似乎还没有想好最合适的办法是什么，因此只提供了一个wmma接口，不说明数据具体在寄存器间的布局。这不仅导致用户无法进一步地在寄存器中处理该矩阵的内容，还无法进行 swizzle 等解决内存布局的冲突。

除了 Tensor Core，很多基本的算法也对寄存器的布局有一定要求，即要求所涉及的操作数在同一线程。例如，要想计算矩阵在一行或一列的最大值，需要把分布在多个线程的数据集中到同一个线程。这样的线程间的寄存器重排都要么依赖于共享内存，要么需要大量的寄存器洗牌才能完成，然而共享内存的带宽基本被 Tensor Core 占满，寄存器洗牌的吞吐也仅为 32/SM/周期并且只可支持一对一洗牌，因此逻辑布局与寄存器布局间的矛盾难以调和。或许什么时候 GPU提供多对多的洗牌功能，或是增大洗牌吞吐，就可以大量降低软件编写的困难。实际上，英伟达也在 Ampere 结构中加入了线程束级的整数归约，合适的时候可以避免大量洗牌。